원주율, 원의 둘레, 원의 넓이, 호의 길이, 부채꼴의 넓이 (공식)

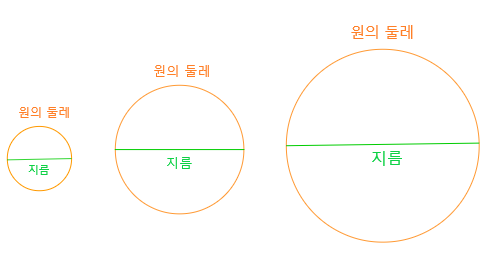
위의 그림에서처럼 원의 크기에 관계없이 원의 둘레는 지름보다 약 3배 정도 큽니다.

초등학교 때는 약 3.14배 정도 크다고 해서 원의 둘레=지름×3.14 라고 배웠었죠.

 

정확히는 원의 둘레는 원의 지름의 3.141592··· 배이며,

3.141592··· 를 원주율이라고 하고 기호로는 $\pi$, 읽을 때는 파이라고 합니다.

 

원의 둘레=지름×원주율

즉 원의 지름의 길이에 대한 원의 둘레의 길이(원주)의 비율을 원주율($\pi$)이라고 합니다.

 

초등학교 때 배운 원주와 원의 넓이를 구하는 공식을 기호로 표현해보도록 해요.

원의 반지름을 r이라고 할 때,

 

원주=2×반지름×3.14 (초등)

원주=2×r×$\pi$

       =2$\pi$r  (공식 ①)

 

원의 넓이=반지름×반지름 ×3.14 (초등)

원의 넓이=r×r×$\pi$

              =$\pi r^2$  (공식 ②)

 

이라고 할 수 있습니다.

 

  부채꼴의 호의 길이와 넓이

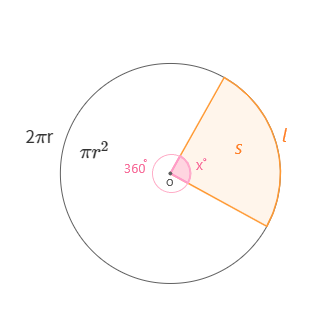
부채꼴의 호의 길이와 넓이는 중심각의 크기에 정비례한다고 했어요.

[이전 글 보기] - 중심각과 호의 길이, 부채꼴의 넓이, 현의 길이 사이의 관계

 

따라서 비례식을 세워 비례식의 외항의 곱과 내항의 곱이 같다는 성질을 이용하면,

부채꼴의 호의 길이와 넓이를 구하는 공식을 유도할 수 있어요.

 

부채꼴의 중심각의 크기를 $x^{\circ }$ , 호의 길이를 ℓ, 부채꼴의 넓이를 S 라고 하면 아래와 같이 나타낼 수 있습니다.

 

360 : x = 2$\pi$r : ℓ

360×ℓ=x×2$\pi$r

ℓ=2$\pi$r×$\frac{x}{360}$  (공식 ③)

 

360 : x = $\pi r^2$ : S

360×S=x×$\pi r^2$

S=$\pi r^2$×$\frac{x}{360}$  (공식 ④)

 

위의 공식을 암기할 때는 부채꼴이 원에서 차지하는 비율을 생각하면 돼요.

즉 부채꼴은 원의 $\frac{x}{360}$배이므로

호의 길이는 원주(2$\pi$r)의 $\frac{x}{360}$배,

부채꼴의 넓이는 원의 넓이($\pi r^2$)의 $\frac{x}{360}$배라고 이해하면 됩니다.

 

또한 부채꼴의 넓이를 호의 길이로 나타낼 수도 있어요.

$\pi r^2$ = $\frac{1}{2}$×r×$2\pi r$ 이므로

 

S=$\pi r^2$×$\frac{x}{360}$

 =$\frac{1}{2}$×r×($2\pi r$×$\frac{x}{360}$)

 =$\frac{1}{2}$rℓ  (공식 ⑤)

입니다.

 

예) 아래의 그림은 한 변의 길이가 10cm인 정오각형의 각 변을 반지름으로 하는 부채꼴과 한 변을 지름으로 하는 반원을 나타낸 것이다. 색칠한 부분의 둘레의 길이와 넓이는?

우선 부채꼴의 호의 길이와 넓이를 구하려면 중심각의 크기를 알아야겠죠?

정오각형의 한 내각의 크기는 $\frac{{180}^{\circ }\times (5-2)}{5}={108}^{\circ }$이므로 부채꼴의 중심각의 크기는 ${360}^{\circ }-{108}^{\circ }={252}^{\circ }$입니다.

[이전 글 보기] - 다각형의 내각의 크기의 합, 정다각형의 한 내각의 크기 (공식)

 

① 색칠한 부분의 둘레의 길이

=(정오각형의 둘레의 길이)+(반지름이 10이고 중심각의 크기가 ${252}^{\circ }$인 부채꼴 2개의 호의 길이)+(지름이 10인 반원의 둘레의 길이)

 

=(5×10)+(2$\pi$×10×$\frac{252}{360}$×2)+(10$\pi$×$\frac{1}{2}$)

=50+28$\pi$+5$\pi$

=50+33$\pi$

 

② 색칠한 부분의 넓이

=(반지름이 10이고 중심각의 크기가 ${252}^{\circ }$인 부채꼴 2개의 넓이)+(지름이 10인 반원의 넓이)

 

=($\pi$×${10}^2$×$\frac{252}{360}$×2)+($\pi$×$5^2$×$\frac{1}{2}$)

=140$\pi$+$\frac{25\pi }{2}$

=$\frac{305\pi }{2}$

 

<참고: 호도법 (고등학교 과정) >

 

$x^{\circ }$=$\theta$(라디안) , ${360}^{\circ }$=2$\pi$(라디안)

 

육십분법 : ℓ=2$\pi$r×$\frac{x^{\circ }}{{360}^{\circ }}$

  호도법 : ℓ=2$\pi$r×$\frac{\theta }{2\pi }$=r$\theta$

 

육십분법 : S=$\pi r^2$×$\frac{x^{\circ }}{{360}^{\circ }}$

  호도법 : S=$\pi r^2$×$\frac{\theta }{2\pi }$=$\frac{1}{2}{r}^2\theta$